정보처리기사 공부를 하는 도중, 여러 가지 정렬 알고리즘에 대해 정리를 할 필요가 있어 이 글을 쓰게 되었다.
정렬 알고리즘은 컴퓨터 분야에서 중요시되는 문제 가운데 하나로 어떤 데이터들이 주어졌을 때 이를 정해진 순서대로 나열하는 문제이다.
정렬 알고리즘 중 주요 알고리즘인 5가지에 대해 정리를 해보려고 한다.
1. 삽입 정렬 (Insertion Sort)
2. 선택 정렬 (Selection Sort)
3. 버블 정렬 (Bubble Sort)
4. 퀵 정렬 (Quick Sort)
5. 힙 정렬 (Heap Sort)
삽입 정렬(Insertion Sort)
삽입 정렬은 가장 간단한 정렬 방식으로 이미 순서화된 파일에 새로운 하나의 레코드를 순서에 맞게 삽입시켜 정렬한다.
N번째 키를 앞의 N-1개의 키와 비교하여 알맞은 순서에 삽입하여 정렬하는 방식이다.
삽입정렬 진행 방식
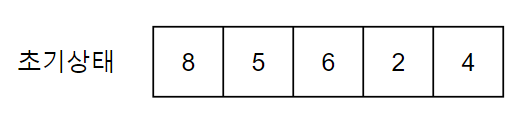

- 두번째 값을 첫 번째 값과 비교하여 5를 첫 번째 자리에 삽입하고 8을 한 칸 뒤로 이동시킨다.

- 세 번째 값을 첫 번째, 두 번째 값과 비교하여 6을 8자리에 삽입하고 8은 한 칸 뒤로 이동시킨다.

- 네 번째 2를 처음부터 비교하여 맨 처음에 삽입하고 나머지를 한 칸씩 뒤로 이동시킨다.

- 다섯 번째 값 4를 처음부터 비교하여 5자리에 삽입하고 나머지를 한 칸씩 뒤로 이동시킨다.
평균과 최악 모두 수행 시간 복잡도는 O(n^2)이다.
삽입 정렬 Java 소스코드
public class Insertion_Sort {
public static void insertion_sort(int[] a) {
insertion_sort(a, a.length);
}
private static void insertion_sort(int[] a, int size) {
for(int i = 1; i < size; i++) { //1.
int target = a[i];
int j = i - 1;
while(j >= 0 && target < a[j]) { //2.
a[j + 1] = a[j];
j--;
}
a[j + 1] = target; //3.
}
}
}
장점
- 알고리즘이 단순하다.
- 대부분의 원소가 이미 정렬되어 있는 경우, 매우 효율적일 수 있다.
- 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다.
- 안장 정렬(Stable Sort)이다.
단점
- 평균과 최악의 시간복잡도가 O(n^2)으로 비효율적이다.
- 데이터의 상태에 따라서 성능 편차가 매우 크다.
선택 정렬(Selection Sort)
선택 정렬은 n개의 레코드 중에서 최소값을 찾아 첫 번째 레코드 위치에 놓고, 나머지 (n-1) 개 중에서 다시 최솟값을 찾아 두 번째 레코드 위치에 놓는 방식을 반복하여 정렬하는 방식이다.
선택정렬 진행 방식
1. 주어진 배열 중에 최소값을 찾는다.
2. 그 값을 맨 앞에 위치한 값과 교체한다.
3. 맨 처음 위치를 뺀 나머지 배열을 같은 방법으로 교체한다.

평균과 최악 모두 수행 시간 복잡도는 O(n^2)이다.
선택 정렬 Java 소스코드
public class Selection_Sort {
public static void selection_sort(int[] a) {
selection_sort(a, a.length);
}
private static void selection_sort(int[] a, int size) {
for(int i = 0; i < size - 1; i++) { //1.
int min_index = 1;
for(int j = i + 1; j< size; j++) { //2.
if(a[j] < a[min_index]) { //3.
min_index = j;
}
}
//4.
swap(a, min_index, i);
}
}
private static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
장점
- 알고리즘이 단순하다.
- 추가적인 메모리 소비가 작다.
단점
- 시간복잡도가 O(n^2)으로, 비효율적이다.
- 불안정 정렬(Unstable Sort)이다.
버블 정렬(Bubble Sort)
버블 정렬은 주어진 파일에서 인접한 두 개의 레코드 키 값을 비교하여 그 크기에 따라 레코드 위치를 서로 교환하는 정렬 방식이다.
계속 정렬 여부를 플래그 비트(f)로 결정한다.
버블 정렬 진행 방식
1. 앞에서부터 현재 값과 바로 다음 값을 비교한다.
2. 현재 값이 다음 값보다 크면 값을 교환한다.
3. 다음 값으로 이동하여 해당 값과 그다음 값을 비교한다.
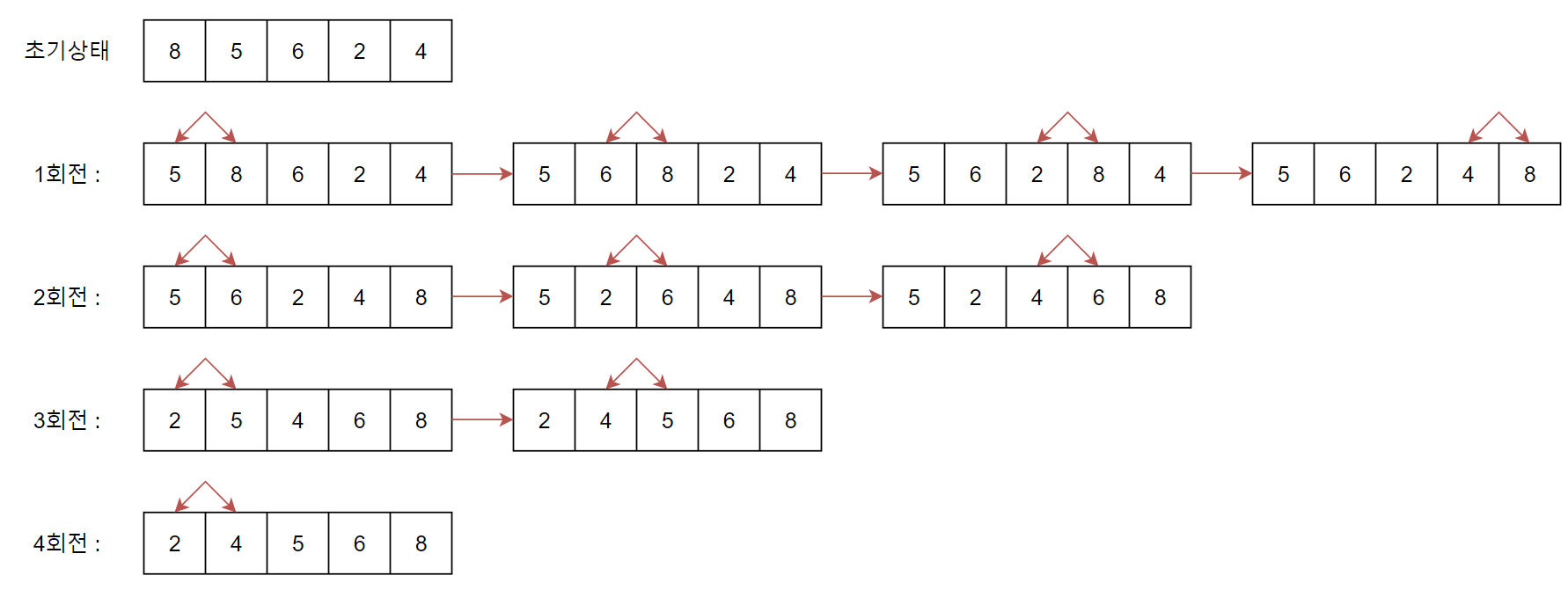
평균과 최악 모두 수행 시간 복잡도는 O(n^2)이다.
버블 정렬 Java 소스코드
Public class Bubble_Sort {
public static void bubble_sort(int[] a) {
bubble_sort(a, a.length);
}
private static void bubble_sort(int[] a, int size) {
for(int i = 1; i < size; i++) {
for(int j = 0; j < size - i; j++) {
if(a[j] > a[j + 1]) {
swap(a, j, j + 1);
}
}
}
}
private static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
장점
- 구현이 매우 간단하고, 소스코드가 직관적이다.
- 추가적인 메모리 소비가 작다.
- 안정 정렬(Stable Sort)이다.
단점
- 시간복잡도가 최악, 최선, 평균 모두 O(n^2)으로, 굉장히 비효율적이다.
- 다른 정렬 알고리즘에 비해 교환 과정이 많아 많은 시간을 소비한다.
퀵 정렬 (Quick Sort)
퀵 정렬은 레코드의 많은 자료 이동을 없애고 하나의 파일을 부분적으로 나누어 가면서 정렬하는 방법으로 키를 기준으로 작은 값은 왼쪽에, 큰 값은 오른쪽 서브파일로 분해시키는 방식으로 정렬한다.
위치에 관계없이 임의의 키를 분할 원소로 사용할 수 있고, 정렬 방식 중에서 가장 빠른 방식이다.
퀵 정렬에서는 재귀를 사용하기 때문에 스택(Stack)이 필요하다.
분할(Divide)과 정복(Conquer)을 통해 자료를 정렬함으로써,
퀵 정렬은 기본적으로 '분할 정복 (Divide and Conquer)' 알고리즘을 기반으로 정렬되는 방식이다.
- 분할(Divide) : 기준 값인 피봇(Pivot)을 중심으로 정렬할 자료들을 2개의 부분집합으로 나눈다.
- 정복(Conquer) : 부분집합의 원소들 중 피봇(Pivot)보다피봇(Pivot) 보다 작은 원소들은 왼쪽, 피봇(Pivot) 보다 큰 원소들은 오른쪽 부분집합으로 정렬한다.
- 부분 집합의 크기가 더 이상 나누어질 수 없을 때까지 분할과 정복을 반복 수행한다.
분할 정복 알고리즘에 관한 자세한 내용은 바로 전 포스팅에서 확인 할 수 있다.
https://lucy1215.tistory.com/30
[알고리즘] 분할 정복 알고리즘 (Divide and Conquer)
❓분할 정복 알고리즘 (Divide and Conquer) 란? 분할 정복(Divide and Conquer) 알고리즘은 여러 알고리즘의 기본이 되는 해결방법으로, 그대로 해결할 수 없는 문제를 작은 문제로 분할하여 문제를 해결하
lucy1215.tistory.com
퀵 정렬 진행 방식
1. 피벗을 하나 선택한다.
2. 피벗을 기준으로 양쪽에서 피벗보다 큰 값, 혹은 작은 값을 찾는다. 왼쪽에서부터는 피벗보다 큰 값을 찾고, 오른쪽에서부터는 피벗보다 작은 값을 찾는다.
3. 양 방향에서 찾은 두 값을 교환한다.
4. 왼쪽에서 탐색하는 위치와 오른쪽에서 탐색하는 위치가 엇갈리지 않을 때까지 2번으로 돌아가 위 과정을 반복한다.
5. 엇갈린 기점을 기준으로 두 개의 부분리스트로 나누어 1번으로 돌아가 해당 부분리스트의 길이가 1이 아닐 때까지 1번 과정을 반복한다.( Divide : 분할)
6. 인접한 부분리스트끼리 합친다. (Conquer : 정복)
퀵 정렬 Java 소스코드
정복 (Conquer)
Public void quick_sort(int[] a, int left, int right) {
if(left >= right) return;
//분할
int pivot = partition();
quick_sort(a, left, pivot - 1); //정복
quick_sort(a, pivot + 1, right); //정복
}
분할 (Divide)
public int partition(int[] a, int left, int right) {
int pivot = a[left];
int i = left;
int j = right;
while(i < j) {
while(pivot < a[j]) {
j--;
}
while(i < j && pivot >= a[i]) {
i++;
}
swap(a, i ,j);
}
a[left] = a[i];
a[i] = pivot;
return i;
}
평균 수행 시간 복잡도는 O(nlog₂n)이고, 최악의 수행 시간 복잡도는 O(n^2)이다.
장점
- 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때 가장 빠르다.
- 추가적인 메모리 공간을 필요로 하지 않는다.
단점
- 불안정 정렬(Unstable Sort)이다.
- 재귀를 사용하지 못하는 환경일 경우 그 구현이 매우 복잡해진다.
힙 정렬 (Heap Sort)
힙 정렬은 전이진 트리(Complete Binary Tree)를 이용한 정렬 방식이다.
구성된 전이진 트리를 Heap Tree로 변환하여 정렬한다.
- 전이진트리는 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리이다.
퀵 정렬 진행 방식
- 문제 : 17, 14, 13,15, 16, 19, 11, 18, 12를 Heap 트리로 구성하시오.
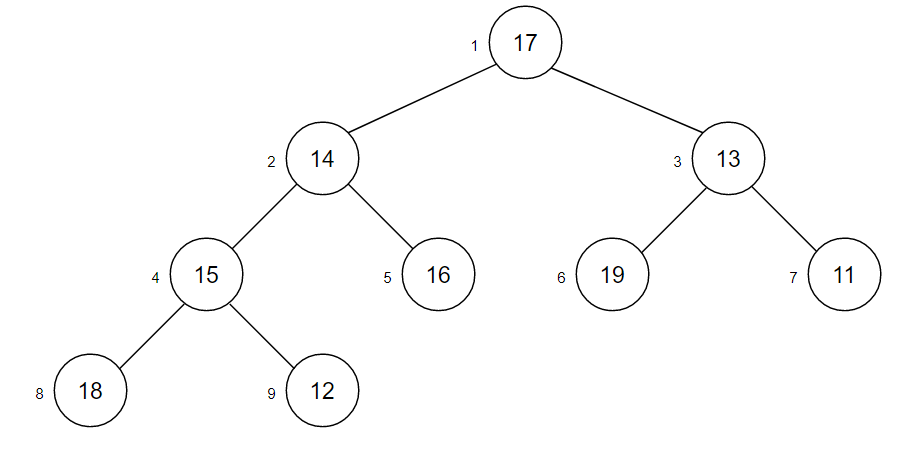
- 주어진 파일의 레코드들을 전이진 트리로 구성한다.
- 전이진 트리의 노드의 역순으로 자식 노드와 부모 노드를 비교하여 큰 값을 위로 올린다.
- 교환된 노드들을 다시 검토하여 위의 과정을 반복한다.
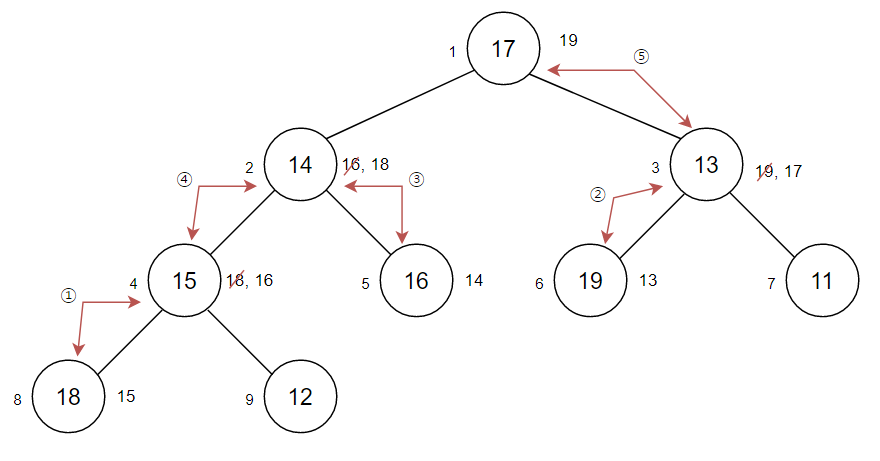


평균과 최악 모두 시간 복잡도는 O(nlog₂n)이다.
힙 정렬 Java 소스코드
private void solve() {
int[] array = { 230, 10, 60, 550, 40, 220, 20 };
heapSort(array);
for (int v : array) {
System.out.println(v);
}
}
public static void heapify(int array[], int n, int i) {
int p = i;
int l = i * 2 + 1;
int r = i * 2 + 2;
if (l < n && array[p] < array[l]) {
p = l;
}
if (r < n && array[p] < array[r]) {
p = r;
}
if (i != p) {
swap(array, p, i);
heapify(array, n, p);
}
}
public static void heapSort(int[] array) {
int n = array.length;
// init, max heap
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(array, n, i);
}
// for extract max element from heap
for (int i = n - 1; i > 0; i--) {
swap(array, 0, i);
heapify(array, i, 0);
}
}
public static void swap(int[] array, int a, int b) {
int temp = array[a];
array[a] = array[b];
array[b] = temp;
}
장점
- 최악의 경우에도 O(nlog₂n)으로 유지가 된다.
- 부분 정렬을 할 때 효과가 좋다
단점
- 일반적인 O(nlog₂n) 정렬 알고리즘에 비해 성능은 약간 떨어진다.
- 안정 정렬이 아니다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 깊이우선탐색(DFS) 과 너비우선탐색(BFS) (2) | 2023.02.21 |
|---|---|
| [알고리즘] 분할 정복 알고리즘 (Divide and Conquer) (2) | 2023.01.29 |
| [알고리즘] 이진 탐색 (Binary Search) (0) | 2023.01.24 |
| [알고리즘] 동적 계획법 (Dynamic Programming) (0) | 2023.01.09 |
| [알고리즘] 그리디 알고리즘 (Greedy Algorithm) (0) | 2023.01.04 |