동적 계획법 관련 문제인 9461번 : 파도반 수열 문제를 풀었다.
동적 계획법에 대해 아직 이해하지 못했다면 다음의 블로그에서 확인하면 된다.
https://lucy1215.tistory.com/23
[알고리즘] 동적 계획법 (Dynamic Programming)
❓동적 계획법 (또는 다이나믹 프로그래밍 , DP)란? 하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 것으로 특정한 알고리즘이 아닌 하
lucy1215.tistory.com
바로 이전, 동적 계획법 관련 문제는 다음의 블로그에서 확인하면 된다.
https://lucy1215.tistory.com/27
[백준] 1904번 : 01타일 (JAVA)
동적 계획법(DP)을 공부한 뒤, DP관련 문제인 1904번 : 신나는 함수 실행을 풀었다. 동적 계획법에 대해 아직 이해하지 못했다면 다음의 블로그에서 확인하면 된다. https://lucy1215.tistory.com/23 [알고리
lucy1215.tistory.com
<문제>
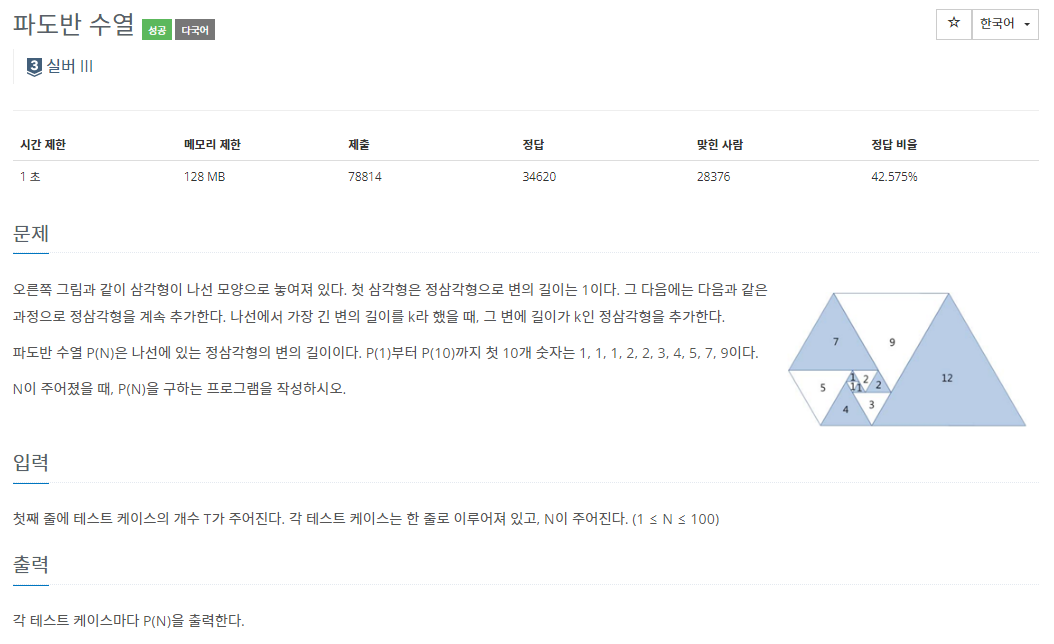

<문제 해석>
동적계획법(DP)를 이용하여 문제의 그림과 같이 삼각형이 만들어지고,
N이 주어질 때, P(N)을 구하라.
<문제 해결>
이번 문제도 규칙만 찾으면 쉽게 해결할 수 있는 동적 계획법 문제였다.
규칙을 찾기위해서 N=1일때부터 삼각형 한 변의 길이를 구해보았다.
P(0) = 0
P(1) = 1
P(2) = 1
P(3) = 1
P(4) = 2
P(5) = 2
P(6) = 3
P(7) = 4
P(8) = 5
그 다음, 문제의 제목인 "파도반 수열" 에 대해 알아보았다.
파도반 수열이란?
N = 1,....에 해당하는 파도반 수열은 아래와 같다.
| 1 | 1 | 1 | 2 | 2 | 3 | 4 | 5 | 7 | 9 |
각 삼각형은 한 변을 두 개의 다른 삼각형과 공유한다.
초기값 P(0) ~ P(2)를 제외하고 P(N) = P(N-2) + P(N-3)임을 알 수 있다.
P(3) = P(1) + P(2) = 1 + 1 = 2
P(4) = P(2) + P(3) = 1 + 1 = 2
P(5) = P(3) + P(4) = 1 + 2 = 3
<코드>
import java.io.IOException;
import java.util.Scanner;
public class Main {
static long dp[];
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
dp = new long[101];
for(int i=0;i<n;i++) {
int a = sc.nextInt();
System.out.println(fibo(a));
}
}
static long fibo(int n) {
dp[0] = 0;
dp[1] = 1;
dp[2] = 1;
dp[3] = 1;
if(dp[n] == 0) {
dp[n] = (fibo(n-3) + fibo(n-2));
}
return dp[n];
}
}
동적계획법만 잘 알고 있으면 쉽게 풀 수 있는 문제였다.
이어서 동적계획법 관련된 문제들을 풀어보겠다.
https://www.acmicpc.net/problem/9461
9461번: 파도반 수열
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의
www.acmicpc.net
'백준' 카테고리의 다른 글
| [백준] 25206번 : 너의 평점은 (JAVA) (0) | 2023.08.13 |
|---|---|
| [백준] 1904번 : 01타일 (JAVA) (0) | 2023.01.18 |
| [백준] 9184번 : 신나는 함수 실행 (JAVA) (0) | 2023.01.12 |
| [백준] 1874번 : 스택 수열 (JAVA) (0) | 2023.01.09 |
| [백준] 4949번 : 균형잡힌 세상 (JAVA) (0) | 2023.01.09 |